pg043CHAPTER II.
REPRESENTATION OF PROPOSITIONS IN TERMS OF x AND m, OR OF y AND m.
§ 1.
Representation of Propositions of Existence in terms of x and m, or of y and m.

Let us take, first, the Proposition “Some xm exist”.
[Note that the full meaning of this Proposition is (as explained at p. 12) “Some existing Things are xm-Things”.]
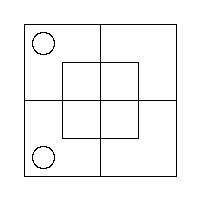
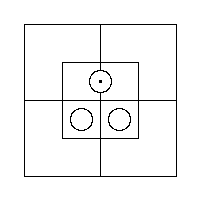
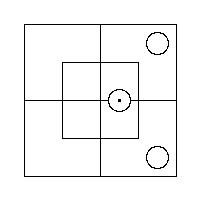
This tells us that there is at least one Thing in the Inner portion of the North Half; that is, that this Compartment is occupied. And this we can evidently represent by placing a Red Counter on the partition which divides it.
[In the “books” example, this Proposition would mean “Some old bound books exist” (or “There are some old bound books”).]
Similarly we may represent the seven similar Propositions, “Some xm′ exist”, “Some x′m exist”, “Some x′m′ exist”, “Some ym exist”, “Some ym′ exist”, “Some y′m exist”, and “Some y′m′ exist”.

pg044Let us take, next, the Proposition “No xm exist”.
This tells us that there is nothing in the Inner portion of the North Half; that is, that this Compartment is empty. And this we can represent by placing two Grey Counters in it, one in each Cell.
Similarly we may represent the seven similar Propositions, in terms of x and m, or of y and m, viz. “No xm′ exist”, “No x′m exist”, &c.
These sixteen Propositions of Existence are the only ones that we shall have to represent on this Diagram.
§ 2.
Representation of Propositions of Relation in terms of x and m, or of y and m.

Let us take, first, the Pair of Converse Propositions
“Some x are m” = “Some m are x.”
We know that each of these is equivalent to the Proposition of Existence “Some xm exist”, which we already know how to represent.
Similarly for the seven similar Pairs, in terms of x and m, or of y and m.

Let us take, next, the Pair of Converse Propositions
“No x are m” = “No m are x.”
We know that each of these is equivalent to the Proposition of Existence “No xm exist”, which we already know how to represent.
Similarly for the seven similar Pairs, in terms of x and m, or of y and m.

pg045Let us take, next, the Proposition “All x are m.”
We know (see p. 18) that this is a Double Proposition, and equivalent to the two Propositions “Some x are m” and “No x are m′ ”, each of which we already know how to represent.
Similarly for the fifteen similar Propositions, in terms of x and m, or of y and m.
These thirty-two Propositions of Relation are the only ones that we shall have to represent on this Diagram.
The Reader should now get his genial friend to question him on the following four Tables.
The Victim should have nothing before him but a blank Triliteral Diagram, a Red Counter, and 2 Grey ones, with which he is to represent the various Propositions named by the Inquisitor, e.g. “No y′ are m”, “Some xm′ exist”, &c., &c.
|
|
|
|
pg050CHAPTER III.
REPRESENTATION OF TWO PROPOSITIONS OF RELATION, ONE IN TERMS OF x AND m, AND THE OTHER IN TERMS OF y AND m, ON THE SAME DIAGRAM.
The Reader had better now begin to draw little Diagrams for himself, and to mark them with the Digits “I” and “O”, instead of using the Board and Counters: he may put a “I” to represent a Red Counter (this may be interpreted to mean “There is at least one Thing here”), and a “O” to represent a Grey Counter (this may be interpreted to mean “There is nothing here”).
The Pair of Propositions, that we shall have to represent, will always be, one in terms of x and m, and the other in terms of y and m.
When we have to represent a Proposition beginning with “All”, we break it up into the two Propositions to which it is equivalent.
When we have to represent, on the same Diagram, Propositions, of which some begin with “Some” and others with “No”, we represent the negative ones first. This will sometimes save us from having to put a “I” “on a fence” and afterwards having to shift it into a Cell.
(1)
“No x are m′;
No y′ are m”.Let us first represent “No x are m′”. This gives us Diagram a.
Then, representing “No y′ are m” on the same Diagram, we get Diagram b.
(2)
“Some m are x;
No m are y”.If, neglecting the Rule, we were begin with “Some m are x”, we should get Diagram a.
And if we were then to take “No m are y”, which tells us that the Inner N.W. Cell is empty, we should be obliged to take the “I” off the fence (as it no longer has the choice of two Cells), and to put it into the Inner N.E. Cell, as in Diagram c.
This trouble may be saved by beginning with “No m are y”, as in Diagram b.
And now, when we take “Some m are x”, there is no fence to sit on! The “I” has to go, at once, into the N.E. Cell, as in Diagram c.
a b c (3)
“No x′ are m′;
All m are y”.Here we begin by breaking up the Second into the two Propositions to which it is equivalent. Thus we have three Propositions to represent, viz.—
(1) “No x′ are m′;
(2) Some m are y;
(3) No m are y′”.These we will take in the order 1, 3, 2.
First we take No. (1), viz. “No x′ are m′”. This gives us Diagram a.
pg052Adding to this, No. (3), viz. “No m are y′”, we get Diagram b.
This time the “I”, representing No. (2), viz. “Some m are y,” has to sit on the fence, as there is no “O” to order it off! This gives us Diagram c.
a b c (4)
“All m are x;
All y are m”.Here we break up both Propositions, and thus get four to represent, viz.—
(1) “Some m are x;
(2) No m are x′;
(3) Some y are m;
(4) No y are m′”.These we will take in the order 2, 4, 1, 3.
First we take No. (2), viz. “No m are x′”. This gives us Diagram a.
To this we add No. (4), viz. “No y are m′”, and thus get Diagram b.
If we were to add to this No. (1), viz. “Some m are x”, we should have to put the “I” on a fence: so let us try No. (3) instead, viz. “Some y are m”. This gives us Diagram c.
And now there is no need to trouble about No. (1), as it would not add anything to our information to put a “I” on the fence. The Diagram already tells us that “Some m are x”.]
|